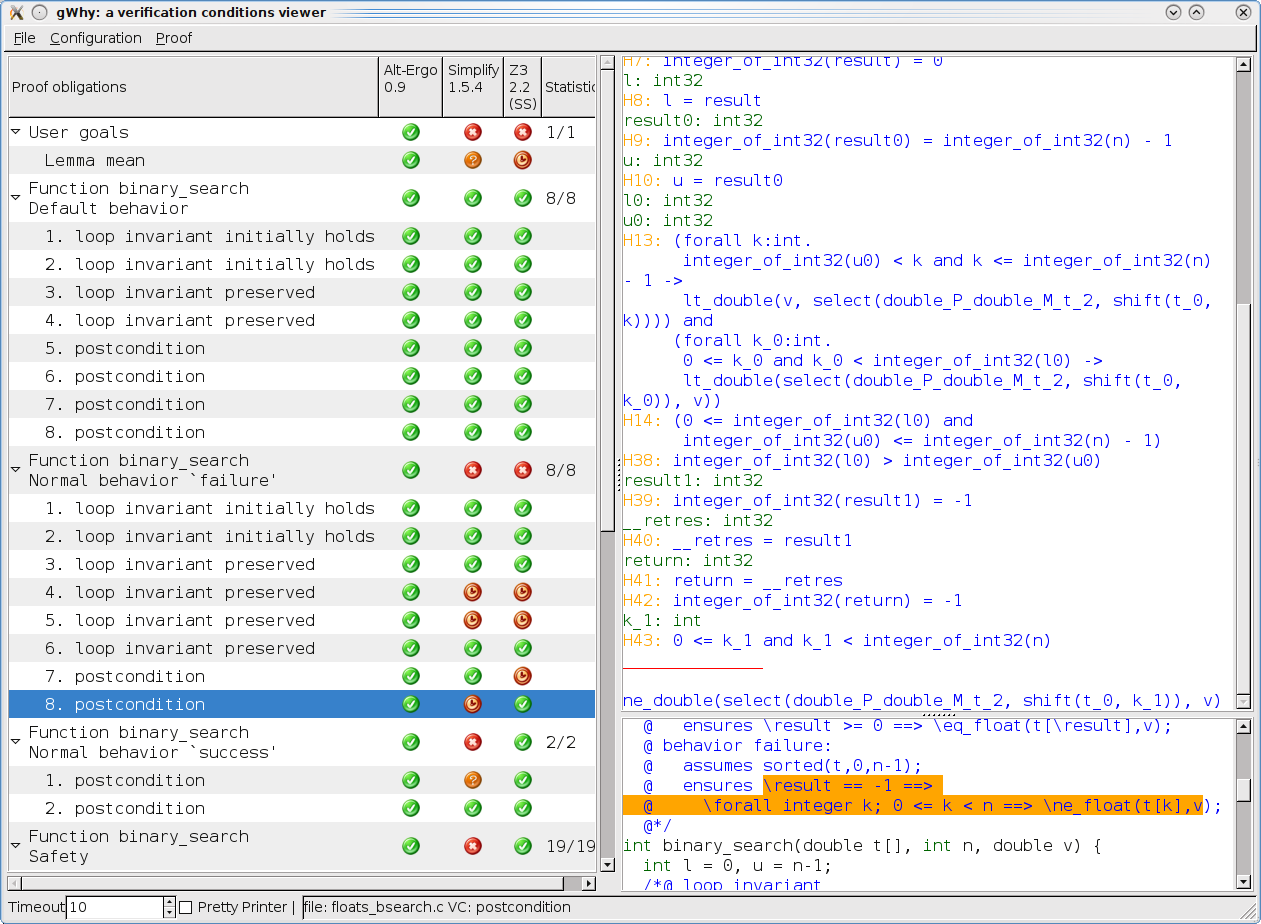
We consider the classical algorithm for searching a value in an array, using a binary search assuming the array is sorted in increasing order.
The originality is that we allow special values for plus and minus infinity to appear in the array. This illustrates how one should be careful with comparison operators. In particular, please notice the use of built-in ACSL predicates for comparing floating-point numbers: \le_float and such. See the ACSL reference manual, section 2.2.5 ``Real numbers and floating point numbers''
#pragma JessieFloatModel(full)
//@ lemma mean: \forall integer x, y; x <= y ==> x <= x+(y-x)/2 <= y;
/*@ predicate sorted{L}(double t[], integer a, integer b) =
@ \forall integer i,j; a <= i <= j <= b ==> \le_float(t[i],t[j]);
@*/
/*@ requires n >= 0 && \valid_range(t,0,n-1);
@ requires ! \is_NaN(v);
@ requires \forall integer i; 0 <= i <= n-1 ==> ! \is_NaN(t[i]);
@ ensures -1 <= \result < n;
@ behavior success:
@ ensures \result >= 0 ==> \eq_float(t[\result],v);
@ behavior failure:
@ assumes sorted(t,0,n-1);
@ ensures \result == -1 ==>
@ \forall integer k; 0 <= k < n ==> \ne_float(t[k],v);
@*/
int binary_search(double t[], int n, double v) {
int l = 0, u = n-1;
/*@ loop invariant
@ 0 <= l && u <= n-1;
@ for failure:
@ loop invariant
@ \forall integer k;
@ 0 <= k < l ==> \lt_float(t[k],v);
@ loop invariant
@ \forall integer k;
@ u < k <= n-1 ==> \lt_float(v,t[k]);
@ loop variant u-l;
@*/
while (l <= u ) {
int m = l + (u - l) / 2;
if (t[m] < v) l = m + 1;
else if (t[m] > v) u = m - 1;
else return m;
}
return -1;
}
This is proved entirely by Alt-Ergo prover, and also in part by other SMT solvers. Unlike most other examples of this gallery, we do not need the Gappa prover, since there is not floating-point rounding involved in this program.
