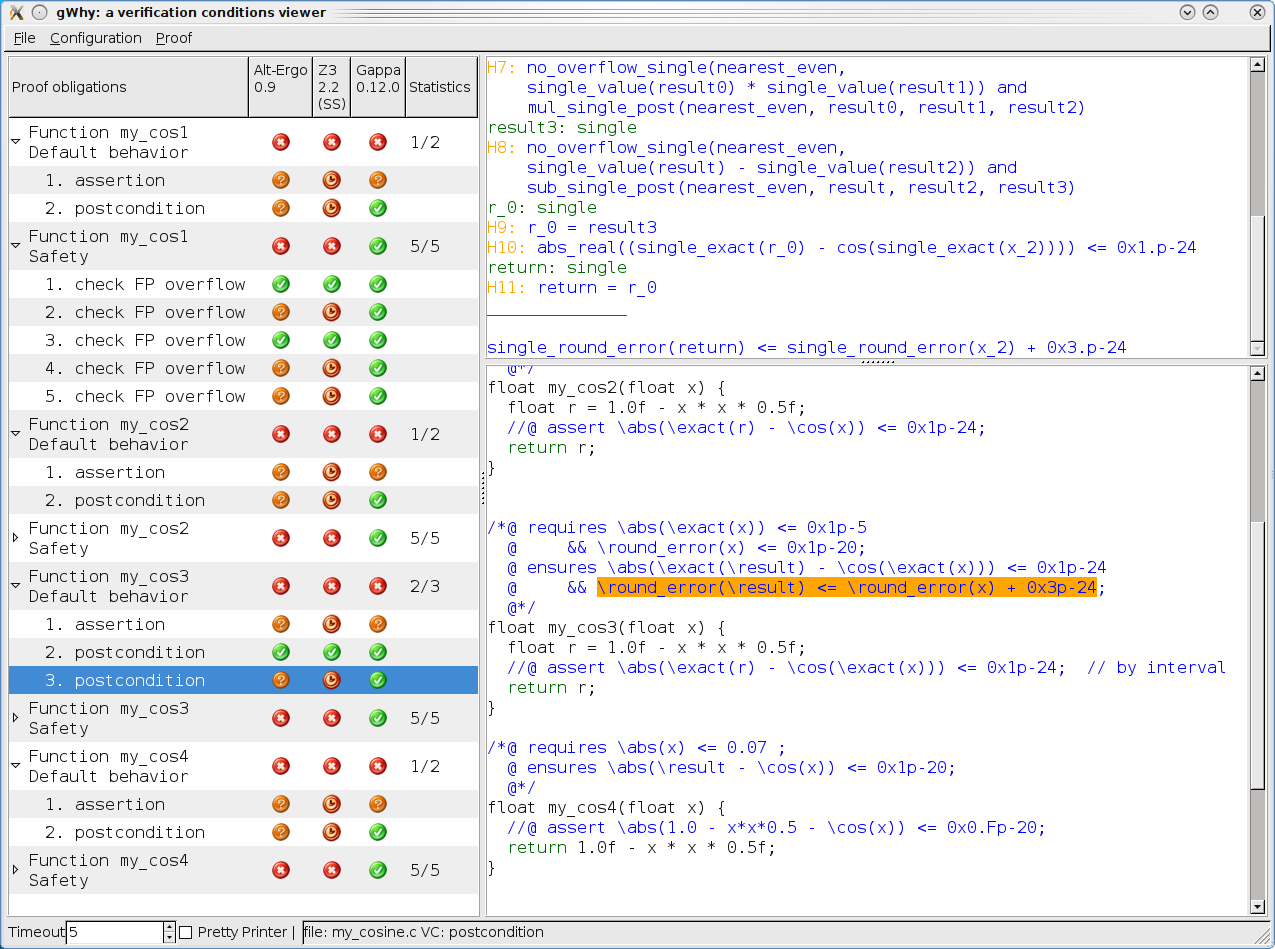
Using Frama-C/Jessie with the strict-IEEE float model, we specify bounds on the total error expected from each function. An assertion in the code is inserted in each function, to express the mathematical error, that is without taking rounding in account.
The third function assumes that the argument is given with an already non-null rounding error, and the error on the result is given in terms of this rounding error on input.
#pragma JessieFloatModel(strict)
/*@ requires \abs(x) <= 0x1p-5;
@ ensures \abs(\result - \cos(x)) <= 0x1p-23;
@*/
float my_cos1(float x) {
//@ assert \abs(1.0 - x*x*0.5 - \cos(x)) <= 0x1p-24;
return 1.0f - x * x * 0.5f;
}
/*@ requires \abs(x) <= 0x1p-5
@ && \round_error(x) == 0.0;
@ ensures \abs(\result - \cos(x)) <= 0x1p-23;
@*/
float my_cos2(float x) {
float r = 1.0f - x * x * 0.5f;
//@ assert \abs(\exact(r) - \cos(x)) <= 0x1p-24;
return r;
}
/*@ requires \abs(\exact(x)) <= 0x1p-5
@ && \round_error(x) <= 0x1p-20;
@ ensures \abs(\exact(\result) - \cos(\exact(x))) <= 0x1p-24
@ && \round_error(\result) <= \round_error(x) + 0x3p-24;
@*/
float my_cos3(float x) {
float r = 1.0f - x * x * 0.5f;
//@ assert \abs(\exact(r) - \cos(\exact(x))) <= 0x1p-24; // by interval
return r;
}
/*@ requires \abs(x) <= 0.07 ;
@ ensures \abs(\result - \cos(x)) <= 0x1p-20;
@*/
float my_cos4(float x) {
//@ assert \abs(1.0 - x*x*0.5 - \cos(x)) <= 0x0.Fp-20;
return 1.0f - x * x * 0.5f;
}
This is proved by a combination of automated provers (SMT solvers and Gappa) and the Coq proof assistant.
The following screenshot shows that SMT solvers and Gappa verify all
verification conditions except the mathematical method errors. The latter
are verified inside Coq using the interval tactic, shown
on the second screenshot below.

Coqide screenshot of proof of first verification condition:
