Clock Drift

The following example is inspired by a famous bug due to clock drift. This showed up dramatically in a patriot missile launcher, and caused several deaths.

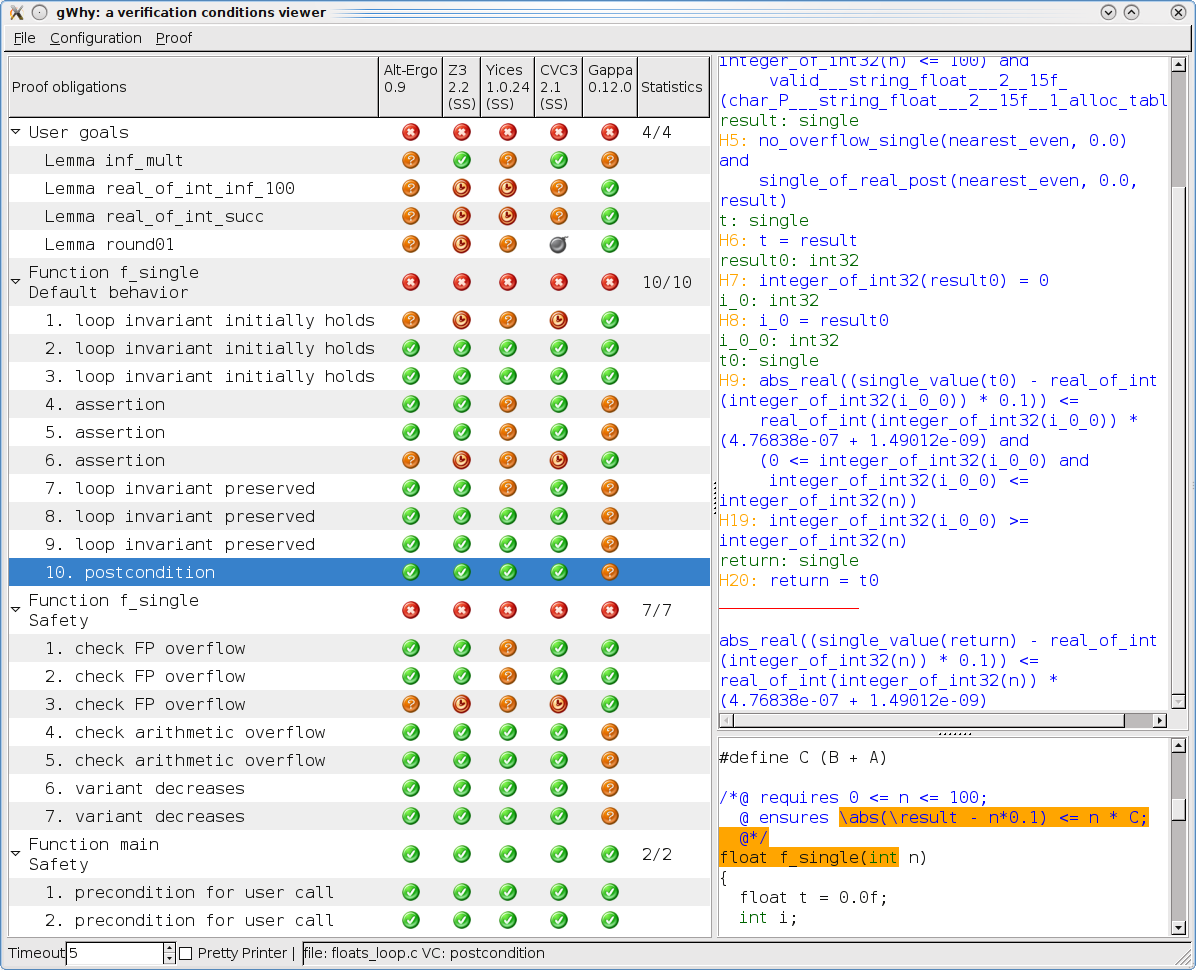
Using Frama-C/Jessie with the strict-IEEE float model, we are able to verify a property on a bound between the computed clock and the expected exact result. We also verify that no overflow can occur.

# pragma JessieFloatModel(strict)

//@ lemma real_of_int_inf_100: \forall integer i; i <= 100 ==> i <= 100.0;

//@ lemma real_of_int_succ: \forall integer n; n+1 == n + 1.0;

//@ lemma inf_mult : \forall real x,y,z; x<=y && 0<=z ==> x*z <= y*z;

#define A 1.49012e-09 
// A is a bound of (float)0.1 - 0.1

//@ lemma round01: \abs((float)0.1 - 0.1) <=  A;

#define B 4.76838e-07
// B is a bound of round_error(t+(float)0.1) for 0 <= t <= 10.01

#define C (B + A)

/*@ requires 0 <= n <= 100;
  @ ensures \abs(\result - n*0.1) <= n * C;
  @*/
float f_single(int n)
{
  float t = 0.0f;
  int i;

  /*@ loop invariant 0 <= i <= n;
    @ loop invariant \abs(t - i * 0.1) <= i * C ;
    @ loop variant n-i;
    @*/
  for(i=0; i < n; i++) {
  L:
    //@ assert 0.0 <= t <= 100.0*(0.1+C)  ;
    t = t + 0.1f;
    //@ assert \abs(t - (\at(t,L) + (float)0.1)) <=  B;
  }
  return t;
}

This is proved by a combination of automated provers: SMT solvers and Gappa, as shown by the following GWhy screenshot.