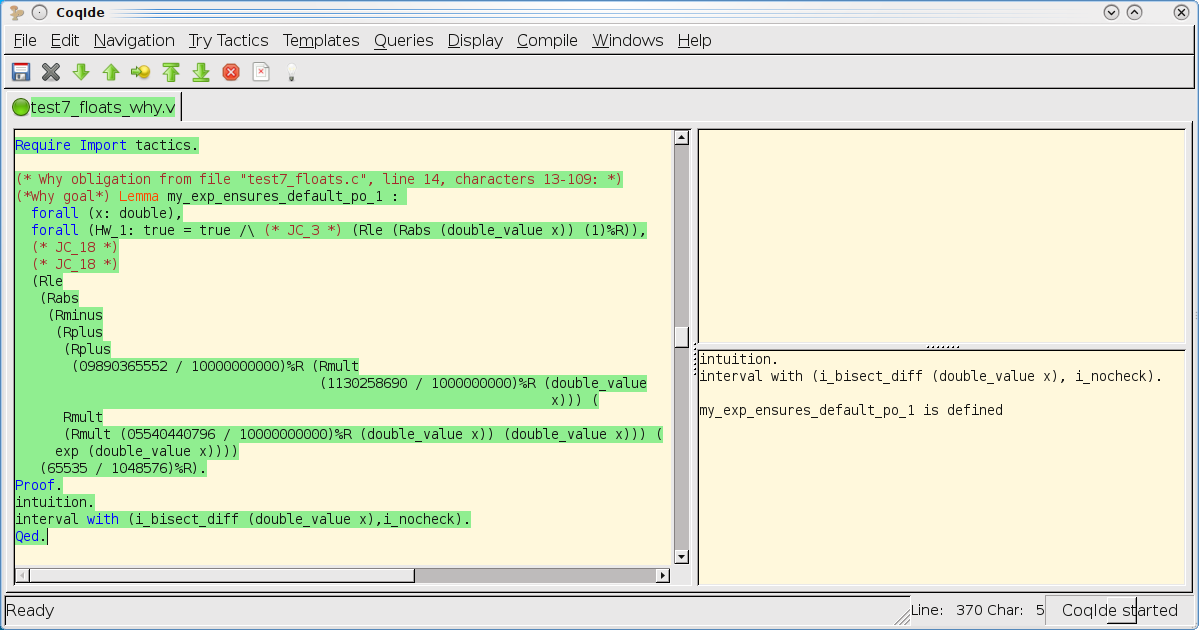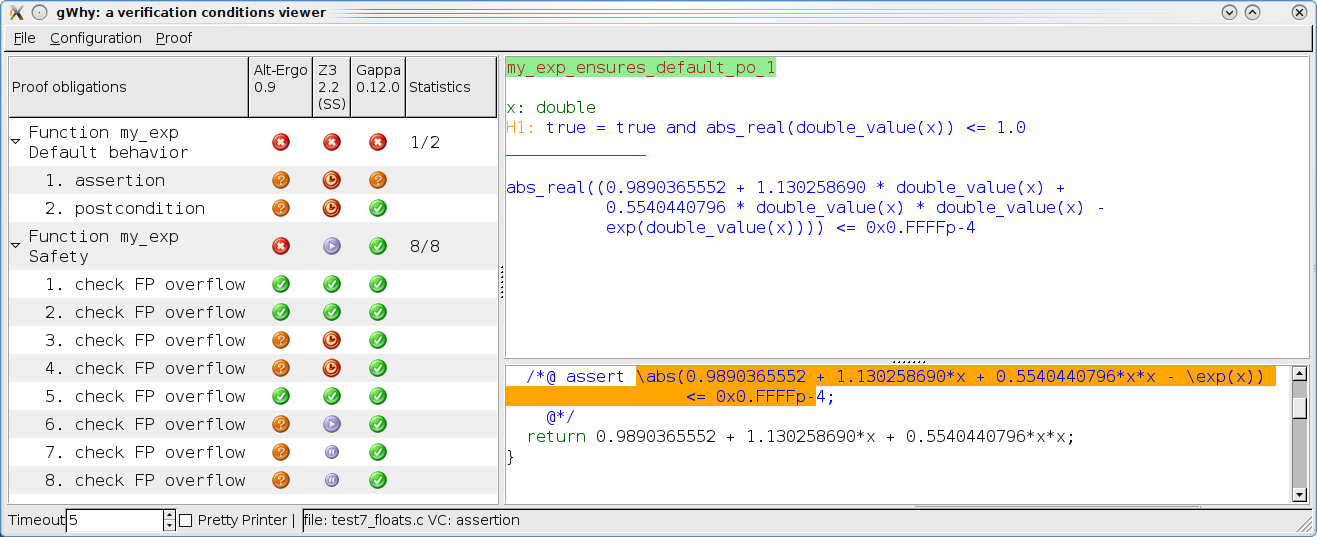
Using Frama-C/Jessie with the strict-IEEE float model, we specify a bound on the total error expected from that function. An assertion in the code is inserted to express the mathematical error, that is without taking rounding in account.
#pragma JessieFloatModel(strict)
/*@ requires \abs(x) <= 1.0;
@ ensures \abs(\result - \exp(x)) <= 0x1p-4;
@*/
double my_exp(double x) {
/*@ assert \abs(0.9890365552 + 1.130258690*x + 0.5540440796*x*x - \exp(x))
<= 0x0.FFFFp-4;
@*/
return 0.9890365552 + 1.130258690*x + 0.5540440796*x*x;
}
This is proved by a combination of automated provers (SMT solvers and Gappa) and the Coq proof assistant.
The following screenshot shows that SMT solvers and Gappa verify all the
verification conditions except the mathematical method error. The latter
is verified inside Coq using the interval tactic, shown
on the second screenshot below.

Coqide screenshot of proof of first verification condition: